优先队列 js 写法 - 每日一题

# 优先队列 js 写法

普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。

而在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出的行为特征。实际上采用的是二叉堆的形式进行存储。由于 js 没有提供现成的优先队列，所以记录一下其 js 的实现过程。

# 思路：

对于一个完全二叉树来说，一个节点的编号为 i （从 0 开始计算），则其父节点的编号为 Math.floor((i-1)/2 , 其左右子节点的编号为 2*i+1 、 2*i+2 。此外对于一个堆来说最重要的就是插入和删除操作。

# 插入

举个例子，假如要在下面的二叉堆（小顶堆）中，再插入 2：

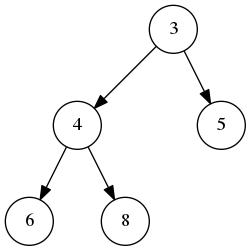
二叉堆插入演示1
首先现在最后插入节点 2

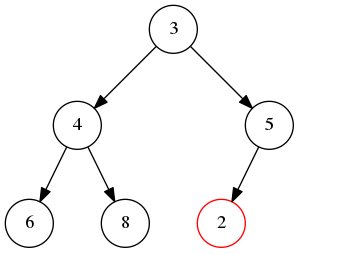
二叉堆插入演示2

然后因为 2 小于 5，不满足堆的性质，上浮

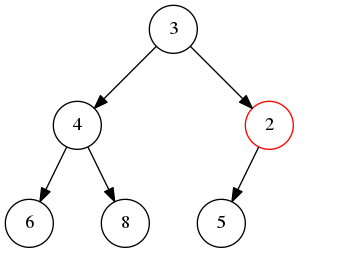
二叉堆插入演示2

然后因为 2 小于 3，不满足堆的性质，继续上浮。最后到顶

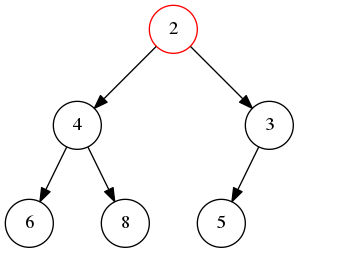
二叉堆插入演示2

# 删除

删除与插入相反，删除的是堆顶元素，我们需要找到一个元素来替代堆顶的位置，以保证堆的性质不被破坏。因此进行如下的操作：

还是以前面建立的二叉堆为例，假如要删除堆顶的 2。则直接先把 2 删除，那么 2 的位置就有一个空穴。

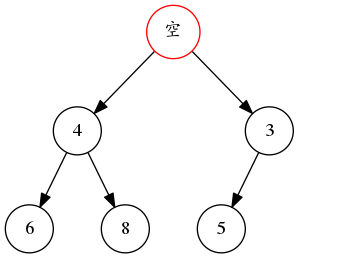
二叉堆删除演示1

然后将 5 替换到空穴的位置，然后因为 5>4>3 不满足小顶堆的性质，所以将 5 和 3 交换。

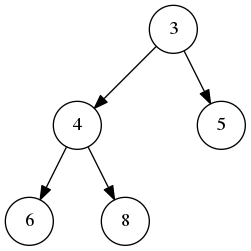
二叉堆删除2

# 代码

	class PriorityQueue {
	constructor(sortBy) {
	// 先把排序方式定下来，默认值是按从小到大排序
	this.sortBy = sortBy \|\| ((a, b) => a - b);
	// 一开始队列的样子，js 中用数组直接表示
	this.queue = [];
	}

	siftUp(index) {
	while (true) {
	let parentIndex = Math.floor((index - 1) / 2);
	console.log("当前", index, "父", parent);
	// 进行上浮
	if (this.sortBy(this.queue[index], this.queue[parentIndex]) < 0) {
	this.swap(index, parentIndex);
	index=parentIndex;
	} else {
	// 终止
	return;
	}
	}
	}
	siftDown(i) {
	let left = i * 2 + 1;
	let right = i * 2 + 2;
	while (true) {
	let maxIndex = i;
	// 左节点是最值的话
	if (
	left <= this.size() &&
	this.sortBy(this.queue[left], this.queue[maxIndex]) < 0
	) {
	maxIndex = left;
	}

	// 右节点是最值的话
	if (
	right <= this.size() &&
	this.sortBy(this.queue[right], this.queue[maxIndex]) < 0
	) {
	maxIndex = right;
	}

	// 如果当前节点不是最值，那么当前节点的值要往下传递，让下面的最值冒泡上来
	if (maxIndex !== i) {
	this.swap(i, maxIndex);
	this.siftDown(maxIndex);
	} else {
	return;
	}
	}
	}

	// 入队 -- 插入元素
	enQueue(node) {
	this.queue.push(node);
	this.siftUp(this.size() - 1);
	this.print();
	}
	print() {
	console.log(this.queue);
	}

	// 出队 -- 获取最值
	deQueue() {
	const top = this.front();
	this.queue[0] = this.queue.pop();
	this.siftDown(0);
	}

	// 获取最值 -- 不移除
	front() {
	return this.queue[0];
	}

	// 获取队列中的元素总数
	size() {
	return this.queue.length;
	}

	// 判断当前优先队列是否为空
	isEmpty() {
	return this.size() === 0;
	}

	// 清空当前队列中的所有元素
	clear() {
	this.queue = [];
	}
	// 交换节点的值
	swap(i, j) {
	const temp = this.queue[i];
	this.queue[i] = this.queue[j];
	this.queue[j] = temp;
	}
	}
	queue = new PriorityQueue();

演示地址：https://codepen.io/memoryoflove/pen/jOaeVxY

leetcode